|
全国各地中小学生已经开始进入寒假复习阶段,各种作业、新知识的预习、旧知识的回顾等等,都等着我们的学生要主动去一个个解决。在复习期间,一些特殊群体是最让很多家长和老师所关注,如我们的初三学子,准中考生们。 虽然全国各地的中考时间都不太一样,但一般都集中在每年的六七月份,算算时间,留给大家的时间并不多了。同时,寒假时间毕竟有限,不可能让大家无限制的复习下去,在有限的时间的里,如何抓住复习重点,这才是每一位准中考生们必须关注和思考的问题。 全国各省市的中考数学试卷相比高考试卷,各地自主命题的权限更大,一般市级教育主管部门就可以进行自主命题。加上数学的教材版本众多,这也给很多考生增加了复习选择资料的难度。 不过,虽然全国各地的中考数学试卷不大相同,但一些重点题型,无论是哪种教材,都会考查,如动点问题。 近几年以来,跟动点有关的问题已经成为考查考生的热点题型,此类问题不仅涉及知识点多,而且能将几何知识和代数知识相互紧密结合在一起,既考查了学生的基本运算能力、又考查了学生的思维能力和空间想象能力。
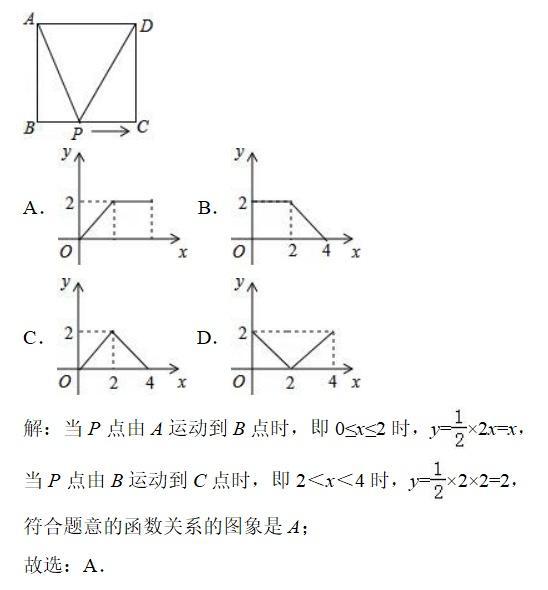
初三生必须复习的重点,动点问题讲解分析1: 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
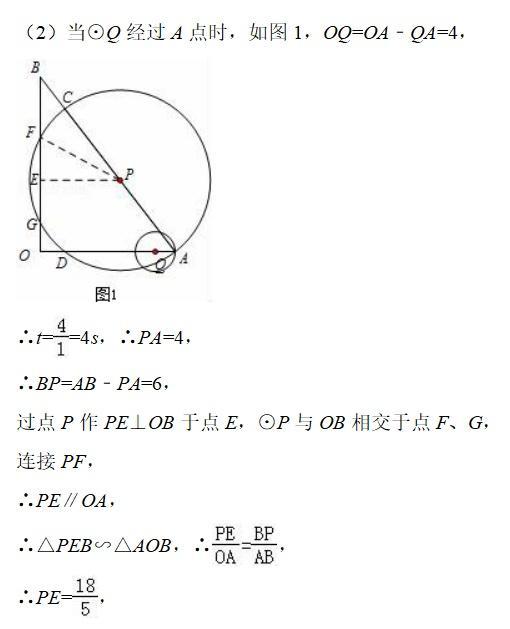
考点分析: 动点问题的函数图象。 题干分析: △ADP的面积可分为两部分讨论,由A运动到B时,面积逐渐增大,由B运动到C时,面积不变,从而得出函数关系的图象。 初三生必须复习的重点,动点问题讲解分析2: 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC。 (1)当t为何值时,点Q与点D重合? (2)当⊙Q经过点A时,求⊙P被OB截得的弦长。 (3)若⊙P与线段QC只有一个公共点,求t的取值范围。
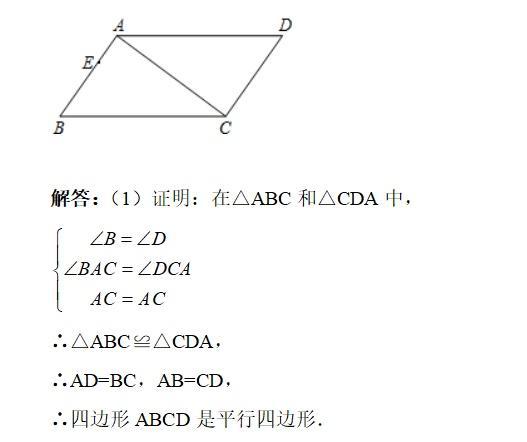
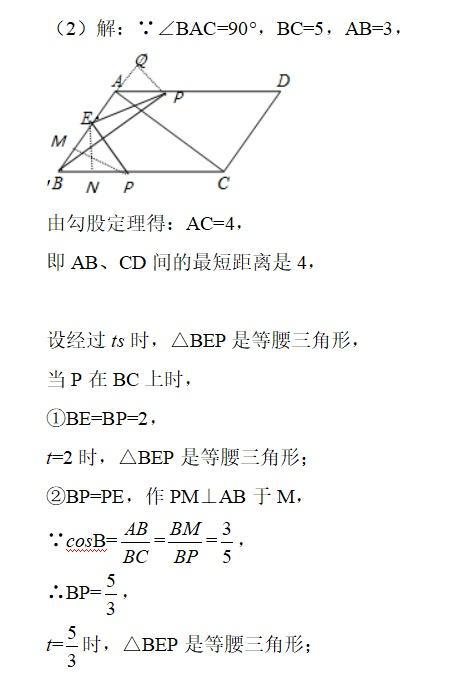
圆的综合题。 题干分析: (1)由题意知CD⊥OA,所以△ACD∽△ABO,利用对应边的比求出AD的长度,若Q与D重合时,则,AD+OQ=OA,列出方程即可求出t的值; (2)由于0<t≤5,当Q经过A点时,OQ=4,此时用时为4s,过点P作PE⊥OB于点E,利用垂径定理即可求出⊙P被OB截得的弦长; (3)若⊙P与线段QC只有一个公共点,分以下两种情况,①当QC与⊙P相切时,计算出此时的时间;②当Q与D重合时,计算出此时的时间;由以上两种情况即可得出t的取值范围。 解题反思: 本题考查圆的综合问题,涉及圆的切线判定,圆周角定理,相似三角形的判定与性质,学生需要根据题意画出相应的图形来分析,并且能综合运用所学知识进行解答。 很多动点类综合问题一般都是以几何基础知识或具体的几何图形作为背景,在几何图形中渗透运动变化的观点,通过点、线、形的运动,图形的平移、翻折、旋转等等把图形的有关性质和图形之间的数量关系和位置关系看作是在变化的、相互依存的状态之中。 初三生必须复习的重点,动点问题讲解分析3: 如图,在四边形ABCD中,∠BAC=∠ACD=90°,∠B=∠D。 (1)求证:四边形ABCD是平行四边形; (2)若AB=3cm,BC=5cm,AE=AB/3,点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,则从运动开始经过多少时间,△BEP为等腰三角形?
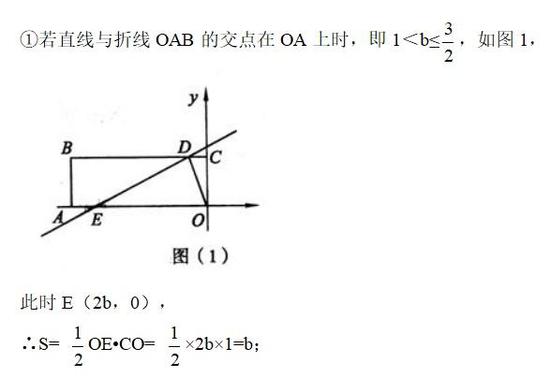
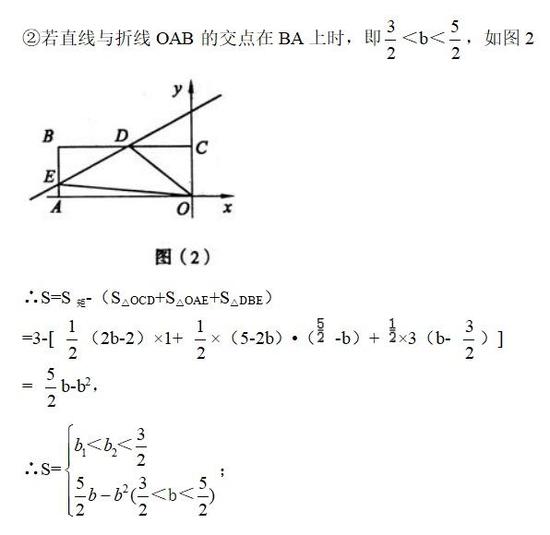
平行四边形的判定与性质;全等三角形的判定与性质;等腰三角形的性质;勾股定理;相似三角形的判定与性质;证明题。 题干分析: (1)根据全等三角形判定证△ABC≌△CDA即可; (2)求出AC,当P在BC上时,①BE=BP=2,②BP=PE,作PM⊥AB于M,根据cosB求出BP,③BE=PE=2,作EN⊥BC于N,根据cosB求出BN;当P在CD上不能得出等腰三角形;当P在AD上时,过P作PN⊥BA于N,证△NAP∽△ABC,推出PN:AN:AP=4:3:5,设PN=4x,AN=3x,在△EPN中,由勾股定理得出方程(3x+1)2+(4x)2=22,求出方程的解即可。 在中考数学中,与运动变化有关的题型一般都是重难点,以动点几何为背景的压轴题,更是近年来中考压轴题中的一种重要题型。此类问题能将代数与几何的众多知识有效整合,能有效考查学生分析问题和解决问题的能力,较好渗透了分类讨论、数形结合、化归等数学思想。 初三生必须复习的重点,动点问题讲解分析4: 如图所示,四边形OABC是矩形,点A、C的坐标分别为(-3,0),(0,1),点D是线段BC 上的动点(与端点B、C不重合),过点D作直线y=x/2+b交折线OAB于点E。 (1)记△ODE的面积为S,求S与b的函数关系式; (2)当点E在线段0A上时,且tan∠DEC=1/2。若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由。
考点:一次函数综合题。 专题:综合题。 分析:(1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积; (2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化。 点评:本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度。 动点相关问题作为近几年全国各地中考数学试卷中的热点和重难点,在一些省市还是必考内容。 因此,初三学生利用寒假复习的时候,一定要重点关注此类问题,吃透解题方法。如此类试题一个主题分成若干个小问题,由易到难层层递进,较全面地考查每位考生的综合理解和分析问题的能力。 中考作为选拔性的人才考试,一般会从考生的综合素质、数学修养等方面出发,而动点问题刚好可以充分考查考生这些数学素质,自然受到命题老师的青睐。 (此文不代表本网站观点,仅代表作者言论,由此文引发的各种争议,本网站声明免责,也不承担连带责任。) |